Stonehenge, A Temple Restor'd to the British Druids, by William Stukeley, [1740], at sacred-texts.com
Stonehenge, A Temple Restor'd to the British Druids, by William Stukeley, [1740], at sacred-texts.com
Of the cell or adytum of Stonehenge. Of the Surgeons amphitheater, London.
Disputations become cloisters and porticoe's. Let us now with minds free from passion, enter the adytum with an intent to find out its true figure, to examine what it really was, and what it is. And that may easily be done, because (as I said before) as to the trilithons of which it is chiefly compos’d, they are all remaining. Not a bit is lost, but what mischievous and silly people knock off with hammers, to see whether, as the wretched vulgar notion would have it, the stones be factitious. TAB. XVIII. is a design of it, which TAB. XVIII. I made sitting in the center of the grand entrance in the inner circle. This point is properly the door-way or entrance into the adytum, as a wicket or little door, whilst the jambs of the hithermost trilithons present themselves, as the greater door, of above 40 feet wide, 25 cubits. I observe in the old Greek story, many footsteps of the primitive patriarchal way left in their sacred structures, which are parallels to this work before us, and others of our Druids. For instance, Pausanias in atticis speaks of a temple dedicate to Venus, in the front of which, is a wall (as he calls it) built of rude stones. Nevertheless he concludes it to be a very famous work. One may very well imagine, this wall of rude stones is the remnant of some such old work as ours, left for the sacred regard the people had to it, even after art was risen to great height, together with superstition and idolatry. For that the most ancient Greeks had very little of idolatry, any more than our Druids, I shall show when I discourse on that head. Again: the more sacred part of the temple at Hierapolis answering to our Adytum, had no door, tho’ none enter’d therein but the chief priests. Lucian de deâ Syria. I suppose it was in imitation of the ancient usage, without doors to shut or open, as our temple here. For the ancients thought it wrong, to confine the deity, as it were, within any cover’d place: ’till Moses, by God's direction, made a tabernacle cover’d with skins, which was to adumbrate the Messiah Son of God, who was to be cloathed with our nature. And Solomon's
temple was built in imitation of this tabernacle. But before that, the ancients meant no more by temples, or altars, as they were first call’d, than a certain known and conspicuous place, ornamented in a particular manner, that should mark out a kebla, or a place towards which we are to address the Deity, and that for uniformity sake. As the Turks and Arabians do now, who are the descendants of Ishmael, and had this custom from Abraham. Tho’ the supreme Being be omnipresent, yet for our convenience, where time, place, and such kind of circumstances are necessary to a public action, he would have, as it were, the place of his presence made notorious. As in the Jewish dispensation he did in a most extraordinary manner, by the shechinah. And from Solomon's temple, all the rest of the world borrow’d the fashion of temples, properly so call’d, built magnificently and with roofs. For the sacred houses mention’d in scripture before then, were only little chapels, shrines, like our Druids kistvaens, which sometime they carried about in a cart, sometime were fix’d in cities, for publick use; as Beth Dagon, and the like. These were but kistvaens improv’d, niches turn’d into sacella, in imitation of two or three stones in Abraham's altars, which we may well call the kebla, and find many of them among our Druid antiquities.
The cell is form’d by a radius of 12 cubits and a half, from the two centers a and b, as to the inward curve; the outward takes a radius of 15 cubits; for these stones are two cubits and a half thick. The two circles are turn’d into an oval, by a radius of 30 cubits, (after the usual manner) set in the two centers c and d, where the two circles intersect. The former centers are 12 cubits and a half distant from each other, the length of the radius. The same oval is obtain’d by a string of 60 cubits, the ends ty’d together, and turn’d round upon two centers, according to the gardiners method. An oval form’d as this is, upon two centers coinciding with each other's circumference; or, which is the same thing, whose centers are distant from each other the length of their radius, is most natural and most beautiful, being the shape of an egg. Most probably these religious philosophers had a meaning, in thus including an egg-like figure, within a circle, more than mere affectation of variety. Whatever that was, we may reasonably conclude, that from the method in antiquity, of making the kebla of a curved figure, the christians borrowed theirs of turning the east end of their churches in that manner; and that the Druids in the work before us, have produc’d the noblest kistvaen or kebla that is known.
My purpose in drawing many prickt lines upon the plate, is not difficult to be understood. Nor does it require particular explanations. To avoid affectation or tediousness, I leave them to the readers amusement: only observe, that Mr. Webb's equilateral triangles have no hand in forming the cell. The intent of it is very distant from a regular polygon. But that it is incomparably more beautiful; than such a one would have render’d it. It is as a magnificent niche 27 cubits long, and as much broad, measuring in the widest place.
This part is call’d
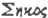[Σηκος ?--JBH] or concha templi and adytum, into which, we may suppose, none but the upper order of priests, together with the high-priest, were commonly to enter, during the time of ministration, in religious rites. We may imagine the beauty of the appearance here upon those occasions, when an innumerable company of the Druids assisted, all in white surplices. The center of the excentricity of this oval is but three cubits nearer the entrance, than the center of the whole work. And they have cut off but one trilithon, which they make the opening of the adytum; meeting the eye to great advantage, from the grand entrance. By the aforesaid contrivance, there is left a space of five cubits between the jambs of the opening of the adytum, and the inner circle in front, just the same as is between the inner and outer circle. The inner circle there performing the office of cancelli to it, as we observ’d before. If a choir of this form was put in practice, and executed by a masterly hand, it would have a very extraordinary effect, and perhaps excel the too similar concave
Click to enlarge
Plate 13. Prospect of STONEHENGE from the Southwest
concave of a cupola. Our Druids had undoubtedly such a notion, in placing this within a circle. And for the sake of this, they turn’d the two circles into a smaller species of an ellipsis.
There's a Druid antiquity like our adytum in shape, call’d Eglwys Glominog, on the top of Arennig vaur in Lhanykil parish, Merionydhshire, but made of a continued wall. The ancients thought the world of an egg-like shape, and as the world is the temple of the Deity, they judg’d it proper to form their temples, so as to have a resemblance thereto. The ancient hieroglyphic of the Deity is a circle, and I have reason to believe it more ancient than the flood. Plato, who learnt much from the ancestors of our Druids, says in Diogenes Laertius, that God is spherical, which he must mean hieroglyphically. So our Druids, as well as he, may mean the infinity of nature in the Deity, who made the world, by this scheme of Stonehenge; at least they understand by the circle, the seat and residence of the Deity, the heavens, which include all things.
It seems to me, that Inigo Jones from this adytum projected the plan of the Surgeons theatre in London, a fabric for seeing and hearing much admired by all good judges. And which my Lord Burlington, out of a spirit truly noble, and a great love for the architect's memory, has lately repair’d, with his own charges and excellent skill. I find the Surgeons theatre (or rather amphitheatre) is form’d from the same proportion as our adytum, the transverse and conjugate diameters being as 4 to 3, viz. 40 foot and 30 foot. And this appears to me a strong presumption, that Inigo Jones did not make the ground-plot of Stonehenge, publish’d under his name. The Surgeons amphitheatre is a good deal less than our cell.
Such is the noble and easy geometry of the adytum of Stonehenge. The stones that compote it, are really stupendous, their height, breadths and thickness are enormous, and to see so many of them plac’d together, in a nice and critical figure, with exactness; to consider, as it were, not a pillar of one stone, but a whole wall, a side, an end of a temple of one stone; to view them curiously, creates such a motion in the mind, which words can’t express. One very remarkable particular in the construction of this adytum, has escaped all observers: which is this. As this part is compos’d of trilithons (as I before call them) sett two and two on each side, and one right before; they rise in height and beauty of the stones, from the lower end of the adytum, to the upper end. My meaning is this. The two hithermost trilithons corresponding, or those next the grand entrance, on the right hand, and on the left are exceeded in height, by the two next in order; and those are exceeded by the trilithon behind the altar, in the upper end of this choir. So that in laying down the measures of the parts, that compose this place, the reader must be content to take my word. Mr. Webb's measures cannot be precise in all of them, seeing he knew nothing of this particular; and that his notion of an hexagon, is contradicted by it, as well as by fact. "He says p. 60. the stones of the greater hexagon seven foot and a half in breadth, three foot nine inches thick, and twenty foot high, each stone having one tenon in the middle." His measure of seven foot and a half in breadth, only shews the vastness of the stones, it is no precise measure, for the founders regarded not any preciseness in their breadth: because two together were design’d to make a compages, whereon to set the impost, and this I call a trilithon. Each trilithon stands by its self, independant of its neighbour, not as the stones and imposts of the outer circle, link’d together in a continued corona, by the imposts carried quite round. Indeed the breadth of a stone at bottom is seven feet and a half, which is 4 cubits and a half. Two stones therefore amount to nine cubits, and there is a cubit of interval between them, making in the whole ten cubits. But they were not careful of the particulars, only of the whole, in one of these compages or trilithons.
The stones of the cell are made to diminish very much, towards the top, most apparently with a design, to take off from their weight, and render them what we call top-heavy, in a less degree. Hence the interval between the two upright stones of the compages widens so much upwards. This must certainly contribute very much, to their stability. In assigning 20 foot for their height, Mr. Webb has well taken the medium. A very small matter more than 20 feet makes exactly 12 cubits of the Hebrews, Egyptians and Druids. The reader remembers the proportion I assign’d between the English foot and this cubit. 20 inches and 4/5 make a cubit, therefore 20 feet and 4/5 make 12 cubits. The true case as to the height of the trilithons, is thus TAB. XV. respectively, and which may be seen in TAB. XV. with the harmony and symmetry, in the proportion of the whole. We may observe their gradual rising in height, all from the same base, like pillars of higher orders and more diameters. But the intelligent reader must needs see, that our founders never had sight of Greek or Roman pillars, and never pretended to imitate them, or take any one idea from them. And of these three different orders or degrees of altitude, in these trilithons, one exceeds the other by a cubit. So that their heights respectively are 13 cubits, 14. cubits, 15 cubits.
The imposts of these trilithons are all of the same height. Mr. Webb p. 61. "informs us, the architrave lying on the top of the great stones of the hexagon and mortaised also into them sixteen foot long, 3 foot 9 inches broad, 3 foot 4 inches high." Mr. Webb's 16 foot long, is too scanty, it amounting to 9 cubits and 2 palms, but the intent of the founders was to make these imposts equal both in length and breadth to the foundation of the upright stones that supports them, I mean the two stones at bottom, the sustaining part of the compages, which in its whole breadth makes 10 cubits; and 10 cubits long the imposts are to be assign’d. Most certainly whoever undertake to measure them, whether from those fallen on the ground, or still in their proper place, will be apt to fail in giving them just length. Both because 1. ’tis observable that these imposts are form’d somewhat broader upwards, than in their bottom part; but this may not be taken notice of by every one. This was done very judiciously upon an optical principle, which it is plain the founders were aware of. For a stone of so considerable an elevation, by this means only, presents its whole face in view. Therefore they that measure it at bottom will not take its true length. 2. If they take the dimension, either from a stone still in its proper place, or from one fallen down, they will be very liable to shorten the measure. For in the first case, the upper edge of these imposts, must needs have suffer’d from the weather, in so elevated an exposure, thro’ the space of 2000 years. It is very apparent they have suffered not a little. Large and deep furrows of age are visible all around them. But if they measure those fallen, they must well imagine such have doubly suffered, from weather, and from the people every day diminishing all corners and edges, to carry pieces away with them. So that in this cafe, analogy and symmetry only can supply these defects. Thus we found before, that the breadth of the imposts of the outer circle is equal to their ichnographical breadth: so it is here, being to cubits. Besides, the outer face of these imposts is longer than the inner, as being in the larger circle. Therefore ten cubits is to be understood their medium measure.
Mr. Webb gives it as a general measure, that they are 3 foot 9 inches broad. He has before told us, the uprights which support them were 3 foot 9 thick; take that twice, it makes 7 foot and a half, which he assigns for the breadth, of the uprights. This is all just within a trifle, and it is not expected that he who was not aware of the cubit, by which these works were made, should do it with greater accuracy. The truth of the whole is this: Webb's 7 foot and half is 4 cubits and a half, as we said before; the half of it is 3 foot 9, and a very little more. But this must be taken for the least breadth of the imposts, that
Click to enlarge
Plate 14. The orthographical Section of Stonehenge upon the Cross diameter
at the ends. For in the middle they are somewhat broader. Tho’ the inside faces are strait, yet, as we observ’d, in proper place, of the imposts of the outer circle; so here, they are rounded behind: their outer circumference answering TAB. XI. to the great oval upon which they are founded. So likewise their ends are made upon a radius of that oval, whence the inner face of the impost is somewhat shorter than the outer, and is another reason why their lengths may easily be taken somewhat too short. I have drawn the imposts in their true shape in the ground-plot. The artifice of the tenons and mortaises of these TAB. XI. trilithons and their imposts, what conformity they bear to that of the outer circle, is exceedingly pretty, every thing being done truly geometrical, and as would best answer every purpose, from plain and simple principles. In the bottom face of the impost, if divided into three squares, the two mortaises are made in the middle of the two outermost squares. Draw diagonal lines from corner to corner; where they intersect, is the center of the mortaise; which central distance from one to the other, is seven cubits of the Druid measure. Each tenon is a cubit broad upon its longest diameter, for they are of an oval figure. An admirable contrivance, that the imposts should lie firm upon the heads of the uprights, and keep the uprights steady in their places, to strengthen and adorn. We may remark this pretty device, in the management of the tenons and mortaises. Cut an egg across upon its shortest diameter or conjugate; one half thereof represents the shape of the tenons of the outer circle. Cut it across upon its transverse diameter, one half is the shape of the tenons of the adytum. ’Tis evident the meaning of it is this. The tenons of the outer circle are higher in proportion, than the others, because the imposts are less and lower than the others, and on both accounts more liable to be disturb’d, either by accident or violence, than the others: therefore more caution is us’d for their preservation. This is an instance of art, noble and simple withal. Mr. Webb says the imposts are 3 foot 4 inches high, which is precisely 2 cubits, a sixth part of the height of the medium order of trilithons; as the imposts of the outer circle are a sixth part of the height of the stones of the outer circle. The medium order of trilithons is above 24 foot high, i.e. 14 cubits. The lower order is 13 cubits, viz. those next the entrance. The upper trilithon behind the altar was 15 cubits. Each rising a cubit higher than the other, as we before observ’d.
I promis’d to show the reader what Stonehenge is, and what it was. The latter, I presume, is done in the four prints, TAB. XII, XIV, p. XV, XVI. beingTAB. XII, XIV, XV, XVI. geometric orthographical sections of the whole work, all necessary ways, such as architects prepare in design, when they set about a building. ’Tis wholly needless to spend many words in explaining them. What the work is, of our adytum at present, is shown in the subsequent prints, TAB. XVIII, XXI, XXII. The Vth corresponds with the XIIth. The one shows the front ofXVIII, XXI, XII" the temple when in perfection, the other as now in ruins. The XVIth may be compar’d with XIX and XX. all presenting a view from the adytum toward the entrance. TAB. XVIII. is a contrary view, when one standing by the entrance,TAB. XVIII. looks toward the adytum. The same is presented in Plate VII. which I call a peep into the sanctum sanctorum. XXII. is the same, but a little oblique. This plate shows at present, what the XIVth does in its original. Plate XV and XXI. correspond, showing the adytum on one side, in its perfect, and in its ruinous state. Particularly they explain, what I spoke of, as to the orderly rising of the trilithons in height, one above another, from the lower end to the upper end of the adytum. TAB. XXII. illustrates it, by exhibiting to view,TAB. XXII. the other and most perfect side of the adytum. ’Tis an oblique prospect of it, from the entrance.
The quantity of the solid is well adjusted, in proportioning the stone-work of this adytum, to the intervals upon the ichnography. Each trilithon is 10 cubits, and each interval about 6. The jambs, or vacuum of the entry expand
themselves to 25 cubits, which is about 43 feet. From which measure my Lord Pembroke demonstrated the falsity of Webb's hexagonal scheme, when his Lordship first did me the honour to discourse about Stonehenge. In Mr. Webb's designs, we find two jambs (taking one trilithon away) expand but little above 31 feet, by his own scales. Tho’ I don’t pretend, but that some of my foregoing measures, may here and there possibly vary a little, upon a very strict trial, and where proper judgment is not us’d, because the stones in some parts may protuberate, or great parts of them may have fallen off; yet 10 foot differenceTAB. XIX, XX. from truth cannot be allow’d of. In the Plates XIX and XX. observe the inside of that upright stone, which makes the northern jamb of the chief entrance of the outer circle. A very great piece is fallen off towards the top, which discovers its tenon and the mortaise of the impost above it. And in the management of such prodigious stones as these are, fix’d in the ground, and ramm’d too like posts: ’tis not to be wonder’d at, if by chance we find some little variation. Tho’ for my own part, I observ’d none; rather wonder’d, how it was possible for them, without lewices and the like devices, to set them in their places to such preciseness. And the reader, whole mind has receiv’d no prepossession, cannot but be abundantly satisfy’d, that the multitude of measures I have given from Mr. Webb's own account, are perfectly agreeable to the scale of cubits, deduc’d from works of the Egyptians and others: and that in round and full numbers, not trifling fractions. If we collate the numbers given, with the Roman scale, the measures appear very ridiculous and without design; and that is a sure way of confuting the opinion, of its being a Roman work. But as these stones are generally rough, and by time must suffer in all dimensions, ’tis not practical to take their true measure, without necessary judgment, and relation had to symmetry.
Of these greater stones of the adytum, as I observed before, there are none wanting. They are all on the spot, 10 upright stones, 5 cornishes. The trilithon first on the left hand is entire in situ, but vastly decay’d, especially the cornish. There are such deep holes corroded, in some places, that dawn make their nests in them. The next trilithon on the left hand, is entire, compos’d of three most beautiful stones. The cornish happen’d to be of a very durable kind of English marble, and has not been much impair’d by weather. My Lord Winchelsea and myself took a considerable walk on the top of it, but it was a frightful situation. The trilithon of the upper end of the adytum, was an extraordinary beauty. But alas through the indiscretion probably, of some body digging there, between them and the altar, the noble impost is dislodg’d from its airy seat, and fallen upon the altar, where its huge bulk lies unfractur’d.
[paragraph continues] The two uprights that supported it are the most delicate stones of the whole work. They were, I believe, above 30 foot long, and well chizell’d, finely taper’d and proportion’d in their dimensions. That southward is broke in two, lying upon the altar. The other frill stands entire, but leans upon one of the stones of the inward oval.
The root-end or unhewn part of both, are rais’d somewhat above ground. We cannot be sure of the true height of this, when it was perfect: but I am sure 15 cubits, which I have assign’d, is the lowest. The next trilithon, that toward the west, is intire, except that some of the end of the impost is fallen
Click to enlarge
Plate 15. The Orthographic Section of Stonehenge up on the Chief diameter
clean off; and all the upper edge is very much diminish’d by time. As Lucretius says,
The last trilithon, that on the right hand of the entrance into the adytum, has suffer’d much. The outer upright being the jamb of the entrance, is still standing, the other upright and impost are both fallen forwards into the adytum, and broke each into three pieces. I suppose from digging near it. But from one piece of the impost lying look, in the middle, between the jambs of the adytum, Mr. Webb in the plan of his ruins of Stonehenge (being his 6th Scheme) forms the remains of his imaginary 6th trilithon, supposing it one of the stones of the inner or lesser hexagon, as he calls it. Yet if this fragment was really a stump of such a stone, as he would have it, still it would not create an hexagonal form of the cell, but stand just in the middle of the entrance, and block it up in a very absurd, unseemly, and incommodious a manner. And nothing can be more certain, than that there never was such a thing in being. That stone of the trilithon which is standing, has a cavity in it which two or three persons may sit in, worn by the weather.
Stonehenge is compos’d of two circles and two ovals, respectively concentric. At the distance of two cubits inward from the greater oval, describe another lesser oval, on which the stones of the inner oval are to stand: 19 stones in number, at about the central distance of 3 cubits. This lesser oval is to be describ’d by a string and the 2 centers, as before. Or by 2 circles from a 10 cubit radius, and the 2 centers a and b, as of the other before was spoken. Mr. Webb says, p. 60, "the stones of the hexagon within, 2 foot 6 inches in breadth, one foot and a half thick and 8 foot high, in form pyramidal." His two foot and a half is our cubit and half; for the breadth of these stones; being but a third of the breadth of the stones of the greater oval. And the interval between stone and stone, the same. Their height is likewise unequal, as the trilithon, for they rise in height as nearer the upper end of the adytum. Mr. TAB. XV. Webb's 8 foot assign’d, is a good medium measure, for it is just 4 cubits and 4 palms, the third part of the height of the medium trilithon. From the ruins of those left, we may well suppose, the first next the entrance and lowest were 4 cubits high; the most advanc’d height behind the altar might be five cubits, and perhaps more. The stones are somewhat of what Mr. Webb calls a pyramidal form, meaning that of an Egyptian obelisk, for they taper a little upwards. They are of a much harder sort than the other stones, as we spoke before, in the lesser circle. The founders provided that their lesser bulk should be compensated in solidity. They were brought somewhere from the west. Of these there are only 6 remaining upright. The stumps of two are left on the south side by the altar. One lies behind the altar, dug up or thrown down, by the fall of that upright there. One or two were thrown down probably, by the fall of the upright of the first trilithon on the right hand. A stump of another remains by the upright there, still standing. Their exact measures either as to height, breadth or thickness, cannot well be ascertain’d. For they took such as they could find, best suiting their scantlings, but the stones were better shap’d and taller, as advancing towards the upper end of the cell.